このセクションでは、C/C++ 言語拡張である配列表記の構文とセマンティクスを説明します。
部分配列表記
標準 C/C++ 言語のアプリケーション・コード中に、次のようにセクション演算子を追加します。
section_operator ::= [<lower bound> : <length> : <stride>]
<lower bound>、<length>、<stride> は整数型で、次に示すように整数値のセットを表します。
<lower bound>, <lower bound + <stride>>, …, <lower bound> + (<length> - 1) * <stride>
添字演算子の代わりに、セクション演算子を使用します。 次の例は、len 要素を持つ部分配列です: a[lb], a[lb + str], a[lb + 2*str], …, a[lb + (len-1)*str]
a[lb:len:str]
C/C++ の宣言では、配列の上限ではなく長さで処理されるため、上限の代わりに長さが使用されています。 また、長さを使用することで、簡単に部分配列のサイズを一致させることができます。
連続する部分配列演算子は多次元配列オブジェクトの部分配列を指定します。 <stride> が指定されない場合、デフォルトの 1 が設定されます。 <length> が 1 以下の場合、部分配列は未定義です。 配列宣言により次元が分かっている場合は、配列の全次元を表す [:] を使用することも可能です。 <lower bound> または <length> のいずれかを指定する必要がある場合、両方を指定してください。
| 例 |
|---|
a[0:3][0:4] // 2 次元配列 a の行 0、列 0 から行 2、列 3 まで 12 個の要素 b[0:2:3] // 1 次元配列 b の 0 から 3 の要素 b[:] // 配列 b 全体 |
配列表記の配列宣言
部分配列表記 [:] を活用するためには、コンパイラーは配列オブジェクトの形状とサイズを知らなければなりません。 次の表では、C/C++ で配列と配列オブジェクトへのポインターを宣言するさまざまな方法をまとめています。
| 長さ | 記憶域クラス | 宣言 |
|---|---|---|
| 固定長 | スタティック | static int a[16][128] |
| 自動 | void foo(void) { int a[16][128]; }
|
|
| 引数 | void bar(int a[16][128]); |
|
| ヒープ | int (*p2d)[128]; |
|
| 可変長 (C99) | 自動 | void foo(int m, int n) { int a[m][n]; }
|
| 引数 | void bar(int m, int n, int a[m][n]); |
|
| ヒープ | void bar(int m, int n){ int (*p2d)[n]; }
|
可変長配列 (VLA) 表記は、C99 [ISO/IEC 9899] 機能で、コンパイラー固有の C++ 拡張です。 GNU* gcc とインテル® C++ コンパイラーでサポートされています。
注
コンパイラーで C99 拡張機能が有効になるように、/[Q]std=c99 コンパイラー・オプションを使用する必要があります。
部分配列の宣言において不完全に次元が指定されている場合 (ポインター変数など)、明示的に部分配列の長さを指定する必要があります。 次に例を示します。
| 例 |
|---|
typedef int (*p2d)[128]; p2d p = (p2d) malloc(sizeof(int)*rows*128); p[:][:] // エラー p[0:rows][:] // OK |
演算子マップ
部分配列では、ほとんどの C/C++ 演算子を利用できます: +, -, *, /, %, <, ==, >, <=, !=, >=, ++, --, |, &, ^, &&, ||, !, -(unary), +(unary), +=, -=, *=, /=, *(ポインター逆参照)。 演算子は暗黙的に部分配列オペランドの全要素にマップされます。 異なる要素の演算も実行順序の制限なしに、並列に実行可能です。
演算を行う配列オペランドのランクとサイズは同じでなければなりません。ランクは、部分配列演算子の数として定義されます。サイズは各部分配列の長さです。 スカラーオペランドは、すべてのランクの部分配列全体に自動的にフィルされます。
| 例 |
|---|
a[:] * b[:] // 要素ごとの乗算 a[3:2][3:2] + b[5:2][5:2] // a[3][3]、b[5][5] から始まる a と b の 2x2 行列の加算 a[0:4] + b[1:2][0:4] // ランクサイズの不一致エラー a[0:4][1:2] + b[0][1] // スカラー b[0][1] を部分配列に加算 |
代入マップ
代入演算子は、左辺 (LHS) の部分配列の各要素に並列に適用されます。
| 例 |
|---|
a[:][:] = b[:][2][:] + c; e[:] = d; e[:] = b[:][1][:]; // ランクの不一致エラー a[:][:] = e[:]; // ランクの不一致エラー |
右辺 (RHS) と左辺がオーバーラップする場合の動作は不定です。 左辺への代入前に右辺が評価されるという保証はありません。 左辺と右辺の間にエイリアシングがある場合は、一時部分配列を使用して、左辺への代入前に右辺を評価する必要があります。 ただし、オーバーラップする範囲とストライドが同じ場合は、問題なく代入が行われます。 このセマンティクスにより、最も効率の良いコードを生成することができます。
| 例 |
|---|
a[1:s] = a[0:s] + 1; // オーバーラップしているために動作は不定 temp[0:s] = a[0:s] +1; // 一時部分配列を使用することでこの問題を解決 a[1:s] = temp[0:s]; // エイリアシング a[:] += b[:]; // オーバーラップする部分が同じで、ストライドもともに 1 なので問題なし // a[:] = a[:] + b[:]; |
集約 (Gather) と分散 (Scatter)
部分配列が添字式に直接使用される場合、部分配列の値によって要素のセットが指定されます。
| 例 |
|---|
unsigned index[10] = {0,1,2,3,4,5,6,7,8,9};
float out[10], in[10] = {9,8,7,6,5,4,3,2,1,0};
out[0:5] = in[index[0:5]]; // 集約
out[index[5:5]] = in[0:5]; // 分散
for(int i = 0; i < 5; i++){
cerr << "out[" << i << "]" << out[i] << endl;
} |
分散の部分配列のインデックス値がお互いにオーバーラップする場合、重複する場所の値は同じでなければなりません。そうでない場合、分散後の格納値が未定義になります。
選択したターゲット・アーキテクチャーと、そのアーキテクチャーで集約 (Gather)/分散 (Scatter) 操作が利用可能かどうかによって、コンパイラーは配列表記演算を適切なハードウェア命令にマップします。
配列の暗黙のインデックス
部分配列を使用するコードを記述する際、個々の要素のインデックスを明示的に参照すると便利です。 例えば、単一の値の代わりに要素インデックスの関数を配列に格納します。 概念的には、部分配列演算は相対ランクごとに暗黙のインデックス変数を含むループと考えることができます。 相対ランクごとに、暗黙のインデックス変数の値は 0 ~ (相対ランクのトリプレットの長さ - 1) の範囲になります。 __sec_implicit_index 操作は、指定された相対ランクの暗黙のインデックス変数の値を返します。 次のように宣言され、関数のように動作します。
intptr_t __sec_implicit_index(int relative_rank);
引数は、整数定数式でなければなりません。要素ごとに再評価され、ランク 1 の式に似ていますが、ランクをチェックするため、暗黙のインデックス操作のランクは 0 です。
| 例 |
int A[10], B[10][10]; // A[0] = 0、A[1] = 1、A[2] = 2 の割り当てを行うには、次を使用します: A[:] = __sec_implicit_index(0); // B[i][j] = i+j を割り当てます: B[:][:] = __sec_implicit_index(0) + __sec_implicit_index(1); // __sec_implicit_index は、部分配列の開始値とは // 関係ありません。実際のインデックスは x+i と y+j ですが、// 値は 0 または 1 のいずれかになります。 // B[x][y] = 0^0、B[x][y+1] = 0^1、B[x+1][y] = 1^0、B[x+1][y+1] = 1^1 B[x:2][y:2] = __sec_implicit_index(0) ^ __sec_implicit_index(1); |
リダクション操作
リダクションは部分配列の要素を組み合わせ、スカラー結果を生成します。 部分配列でリダクションをサポートするインテル® Cilk™ Plus は、ユーザー定義の 2 項関数を適用する汎用リダクション関数とリダクション関数の結果を適用するための汎用変異リダクション関数を定義します。 また、インテル® Cilk™ Plus にはビルトインの一般的なリダクション関数が 9 つあります。これらのビルトイン関数は多相関数で、int、float、他の基本的な C データ型引数を使用できます。 これらのリダクション関数の名前と概要は次のとおりです。各関数の詳細と使用例は後述します。
| 関数プロトタイプ | 説明 |
|---|---|
| __sec_reduce(fun, identity, a[:]) | 汎用リダクション関数。identity を初期値として使用し、配列 a[:] に fun を実行します。 非推奨。 |
| result __sec_reduce(initial, a[:], function-id) | スカラー型と C++ 算術クラスをサポートする汎用リダクション関数。 リダクション関数 function-id と初期値 initial を使用して、配列 a[:] のリダクション操作を実行します。 結果は result で返されます。 |
| void __sec_reduce_mutating(reduction, a[:], function-id) | スカラー型と C++ 算術クラスをサポートする汎用変異リダクション関数。 リダクション関数 function-id とレデュース操作 reduction の結果を初期値として使用して、配列 a[:] のリダクション操作を実行します。 戻り値はありません。 |
| ビルトインのリダクション関数 | |
| __sec_reduce_add(a[:]) | 配列として渡された値を加算します。 |
| __sec_reduce_mul(a[:]) | 配列として渡された値を乗算します。 |
| __sec_reduce_all_zero(a[:]) | 配列要素がすべてゼロであるかテストします。 |
| __sec_reduce_all_nonzero(a[:]) | 配列要素がすべて非ゼロであるかテストします。 |
| __sec_reduce_any_nonzero(a[:]) | 非ゼロの配列要素があるかテストします。 |
| __sec_reduce_min(a[:]) | 配列要素の最小値を特定します。 |
| __sec_reduce_max(a[:]) | 配列要素の最大値を特定します。 |
| __sec_reduce_min_ind(a[:]) | 配列要素の最小値のインデックスを特定します。 |
| __sec_reduce_max_ind(a[:]) | 配列要素の最大値のインデックスを特定します。 |
| __sec_reduce_and (a[:]) | 配列として渡された値のビット単位の AND (論理積) 演算を行います。 |
| __sec_reduce_or (a[:]) | 配列として渡された値のビット単位の OR (論理和) 演算を行います。 |
| __sec_reduce_xor (a[:]) | 配列として渡された値のビット単位の XOR (排他的論理和) 演算を行います。 |
汎用リダクション関数: function-id で表される関数には、operator+ のように、演算に加えて代入を必要とするユーザー定義の関数、演算子、関数子、ラムダ式を指定することもできます。 リダクション関数は可換的でなければなりません。部分配列の要素型は、次のことに使用されます。
リダクション関数の解の検索と多重定義
戻り値を結果に代入するための代入演算子
使用するリダクション変数に初期値を代入するためのコピー・コンストラクター (必要な場合)
注
この実装では、非定数関数ポインターをリダクション関数とすることができます。 また、__sec_reduce(fun, identity, a[:]); は古いリダクション関数 (非推奨) です。代わりに、ユーザー定義関数とともに result __sec_reduce(initial, a[:], function-id) を使用できます。 __sec_reduce(fun, identity, a[:]); は将来廃止される予定です。
| 例 |
|---|
... complex<double> a[N]; complex<double> result; ... result = __sec_reduce(complex<double>(0,0), a[:], operator+ ); ... |
汎用変異リダクション関数: function-id で表される関数には、複合代入 operator+= のように、演算に加えて代入を必要とするユーザー定義の関数、演算子、関数子、ラムダ式を指定することもできます。 リダクション関数は可換的でなければなりません。 部分配列の要素型は、複合リダクション関数の解の検索と多重定義に使用されます。
注
変異リダクションには、代入演算子は必要ありません。
| 例 |
|---|
... complex<double> a[N]; complex<double> result; ... result = complex<double>(0,0); __sec_reduce_mutating(result, a[:], operator+= ); ... |
ビルトインのリダクション関数: リダクション演算は複数のランクのリダクションが可能です。 リダクション可能なランクの数は実行コンテキストに依存します。 ランク m の実行コンテキストとランク n のリダクション部分配列引数では (n>m)、部分配列引数の最後の n-m ランクが減らされます。
| 例 |
|---|
sum = __sec_reduce_add(a[:][:]); // 配列 'a' 全体の合計を計算 sum_of_row[:] = __sec_reduce_add(a[:][:]); // 'a' の各行の要素の合計を計算 |
シフト演算
shift は部分配列の要素をシフトして、スカラー結果を生成します。 インテル® Cilk™ Plus は、部分配列でシフト演算をサポートします。 シフト関数の名前と説明は次のとおりです。 シフトおよび循環シフト (回転) 関数は、ランク 1 の式用に定義されています。
| 関数プロトタイプ | 説明 |
|---|---|
| b[:] = __sec_shift(a[:], signed shift_val, fill_val) | 汎用シフト関数。配列 a[:] の要素を上位 (インデックス値が大きくなるよう)/下位 (インデックス値が小さくなるよう) にシフトします。 shift_val が正の場合は下位にシフトし、shift_val が負の場合は上位にシフトします。 fill_val 引数の値は部分配列要素と同じデータ型で、空の要素を埋めるのに使用されます。 結果は戻り値 b[:] に代入されます。 部分配列引数 a[:] は変更されません。 |
| b[:] = __sec_rotate(a[:], signed shift_val) | 汎用回転関数。部分配列 a[:] の要素を循環シフト (回転) します。 shift_val が正の場合は下位にシフトし、shift_val が負の場合は上位にシフトします。 結果は戻り値 b[:] に代入されます。 部分配列引数 a[:] は変更されません。 |
関数マップ
マップはスカラー関数で暗黙的に定義されます。スカラー関数マップ呼び出しの部分配列引数はすべて同じランクでなければなりません。 スカラー引数は、ランクが同じになるように自動で挿入されます。
| 例 |
|---|
a[:] = sin(b[:]); a[:] = pow(b[:], c); // b[:]**c a[:] = pow(c, b[:]); // c**b[:] a[:] = foo(b[:]); // ユーザー定義関数 a[:] = bar(b[:], c[:][:]); // ランクの不一致エラー |
マップされた関数呼び出しは、特定の順序とは関係なく、すべての配列要素に対して並列に実行されます。 ベクトル関数は副作用をもたらすことがあります。並列実行時に競合が発生する場合、プログラムのセマンティクスがシリアルプログラムと異なっている可能性があります。
関数マップは、部分配列のすべての要素に対して演算セットを並列に適用する強力なツールです。
svml ライブラリーの多くのルーチンは、互換マイクロプロセッサーよりもインテル製マイクロプロセッサーでより高度に最適化されます。
部分配列引数の渡し方
インテル® Cilk™ Plus は「ベクトルカーネル」スタイルのプログラミングをサポートしています。これは、固定または引数化されたベクトル長の配列引数を宣言することにより、ベクトルコードが 1 つの関数内にカプセル化されます。
部分配列の最初の要素のアドレスを引数として配列引数に渡すことができます。 次の例は、インテル® Cilk™ Plus のスレッディングを使用して関数呼び出しを並列化し、配列表記を使用して関数本体のベクトル化を行う方法を示します。
注
引数 float x[m] は引数 int m に依存し、C99 でのみサポートされ、C++ ではサポートされません。
| 例 |
|---|
#include <cilk/cilk.h>
void saxpy_vec(int m, float a, float x[m], float y[m]){
y[:]+=a*x[:];
}
void main(void){
int a[2048], b[2048] ;
cilk_for (int i = 0; i < 2048; i +=256){
saxpy_vec(256, 2.0, &a[i], &b[i]);
}
} |
配列引数を明示的に指定して関数を記述することにより、スレッディング・ランタイムとスケジューラーを使用して移植性の高いベクトルコードを記述することができます。
条件文と if 文
部分配列は、C/C++ の条件演算子や if 文の条件のテストで使用できます。
| 例 |
|---|
c[0:n] = (a[0:n] > b[0:n]) ? a[0:n] - b[0:n] : a[0:n];
// 次のコードと同じ
if (a[0:n] > b[0:n]) {
c[0:n] = a[0:n] - b[0:n];
}
else {
c[0:n] = a[0:n];
} |
上記の例では、a[i] > b[i] かどうかに応じて、結果配列 c の各要素 c[i] に a[i]-b[i] または a[i] が代入されます。
条件式 (if 文の条件や条件演算子) で部分配列を使用する場合、"true" および "false" 節のそれぞれの文のすべての部分配列が同じ形状でなければなりません。
条件式の右辺と左辺を計算し混合操作を行うには、ハードウェアが必要になることがあります。節はできるだけ短くします。
制限事項
部分配列の使用については、2 点の制限事項があります。
関数は部分配列の値を返すことはできません。出力値を受け取る方法は 2 つあります。
出力配列:
void addit(float out[N], float in[N]) { out[:] = in[:] + 4.5f; } float A[N],B[N]; addit(A,B);関数マップ:
float addit(float in) { return in + 4.5f; } float A[N],B[N]; A[:] = addit(B[:]);関数がインライン展開されない場合、この 2 つのアプローチの関数呼び出し回数は異なります。 関数マップアプローチのほうが、出力配列アプローチよりも addit()N 回多く呼び出すため、このことを考慮する必要があります。
部分配列を含む条件式の "true" および "false" 節に return、break、while、for、または goto 文を含めてはなりません。 入れ子の if 文は許可されています。
プログラミングのヒントとサンプルプログラム
同じ配列でスカラーとデータ並列操作を組み合わせたアプリケーションの記述に関連するコストはありません。 インテル® コンパイラーはプログラムの配列演算を使用して、ベクトル化を行います。 次の例は FIR フィルターを実装しています。このスカラーコードは、内側も外側もベクトル化が可能な、二重に入れ子されたループからなります。 配列表記を使用して別の方法でプログラムを記述することにより、コンパイラーに別のベクトル化を行うように指示できます。
| FIR スカラーコードの例 |
|---|
for (i=0; i<M-K; i++){
s = 0
for(j=0; j<K; j++){
s+= x[i+j] * c[j];
}
y[i] = s;
} |
| FIR 内側のループをベクトル化する例 |
for (i=0; i<M-K; i++){
y[i] = __sec_reduce_add(x[i:K] * c[0:K]);
} |
| FIR 外側のループをベクトル化する例 |
y[0:M-K] = 0;
for (j=0; j<K; j++){
y[0:M-K]+= x[j:M-K] * c[j];
} |
並列配列代入セマンティクスは、引数の左辺値が右辺のオペランドとエイリアスする場合でも、右辺の演算のベクトル化を有効にします。 コンパイラーはエイリアスの際に自動で一時配列を使用しないため、確実に正しい動作が保証されるように明示的に一時配列を追加すべきです。 この一時配列によりメモリー使用量が増加し、その読み取りと書き込みのオーバーヘッドが発生します。これらは、コードのベクトル化によるスピードアップで相殺する必要があります。
| 例: |
|---|
void saxpy_vec (int m, float a, float *x, float y[m]){
y[:] += a * x[0:m]; // コンパイラーは x と y がオーバーラップしないと仮定するが、実際にはオーバーラップしている
}
void saxpy_vec (int m, float a, float x[m], float y[m]){
float z[m];
z[:] = y[:]; // 確実でない場合は一時配列を使用する
// オーバーラップの可能性があるかどうか確認したほうがよい
y[:] = z[:] + a * x[:];
} |
ベクトル命令セットの利点を活用するには、次の例で示すように、プロセッサーでサポートされる固定ベクトル長を使用すると良いでしょう。 次のコード例は、2 次元グリッドで 9 ポイントの平均を計算します (9 ポイントの平均が定義されていないグリッドの周りの 1 要素の境界は回避します)。 コア演算はベクトル形式で関数 nine_point_average として記述されています。 呼び出しで cilk_for ループを使用することで、アプリケーションはさらに並列化されています。 演算の粒度は、各呼び出しで処理されるベクトル演算の長さと行数を指定する 2 つのコンパイル時定数 VLEN と NROWS により制御されます。 隣接した行のロードは複数の行に渡って再利用されるため、関数内で複数行を処理することによりメモリーの局所性が高まります。 ベクトル演算の長さにコンパイル時定数を使用すると、ベクトルコード生成がより効率的かつ予測可能になります。
| 例 |
|---|
#include <malloc.h>
#include <cilk/cilk.h>
#define VLEN 4
#define NROWS 4
//-------------------------------------------------------------------
// ベクトルカーネル
// 各グリッドに対して次を実行
// o[x][y] = (i[x-1][y-1] + i[x-1][y]+ i[x-1][y+1] +
// i[x][y-1] + i[x][y] + i[x][y+1] +
// i[x+1][y-1] + i[x+1][y] + i[x+1][y+1])/9;
// 次のコンパイル時定数を使用:
// 1) VLEN 列 - ベクトル化
// 2) NROWS 行 - 隣接した行のロードを再利用
//--------------------------------------------------------------------
void nine_point_average(int h, int w, int i, int j, float in[h][w], float out[h][w])
{
float m[NROWS][VLEN];
m[:][:] = in[i:NROWS][j:VLEN];
m[:][:] += in[i+1:NROWS][j:VLEN];
m[:][:] += in[i+2:NROWS][j:VLEN];
m[:][:] += in[i:NROWS][j+1:VLEN];
m[:][:] += in[i+1:NROWS][j+1:VLEN];
m[:][:] += in[i+2:NROWS][j+1:VLEN];
m[:][:] += in[i:NROWS][j+2:VLEN];
m[:][:] += in[i+1:NROWS][j+2:VLEN];
m[:][:] += in[i+2:NROWS][j+2:VLEN];
out[i:NROWS][j:VLEN] = 0.1111f * m[:][:];
}
//---------------------------------------------------------------------
// 呼び出し元
//---------------------------------------------------------------------
const int width = 512;
const int height = 512;
typedef float (*p2d)[];
int main() {
p2d src = (p2d) malloc(width*height*sizeof(float));
p2d dst = (p2d) malloc(width*height*sizeof(float));
// …
// 9 ポイントの平均を計算
cilk_for (int i = 0; i < height - NROWS - 3; i += NROWS) {
for (int j = 0; j < width - VLEN - 3; j += VLEN) {
nine_point_average(height, width, i, j, src, dst);
}
}
} |
| コマンドライン入力 |
icl /Qstd=c99 test.c // Windows® icc -std=c99 test.c // Linux* および OS X* |
配列表記によるベクトル化のデータレイアウトの最適化
一部のアプリケーションでは、構造体配列 (AOS) から配列構造体 (SOA) へデータ構造を変更することで、複数の配列要素にわたる構造体の 1 つのフィールドにアクセスするギャザー操作を回避し、配列を反復するループがコンパイラーによってベクトル化されるようにできます。 各ループの前後でコストがかかる変換を繰り返し行わなくて済むように、このようなデータ変換はプログラムレベルで行うべきです。
AOS から SOA への変換: 構造体配列 (AOS) から配列構造体 (SOA) へデータ構造を変更することは、ベクトル化されるコードにおいてギャザー/スキャッター操作を回避する一般的な最適化です。 構造体フィールドごとに個別の配列を保持することで、連続したメモリーアクセスになり、構造体要素がベクトル化されます。 AOS 構造はギャザーとスキャッターを必要とするため、SIMD の効率性が低下するだけでなく、メモリーアクセスにかかわる帯域幅とレイテンシーが増加します。 一般にギャザー/スキャッター操作は、連続したロードと比べて非常に多くの帯域幅とレイテンシーが要求されるため、ハードウェアでギャザー/スキャッター・メカニズムが利用できる場合であっても、このデータ構造の変更は必要です。
SOA 形式は、オリジナルの構造体要素の複数のフィールドへのアクセスに際して局所性が低下するため、TLB (トランスレーション・ルックアサイド・バッファー) の負担が増加します。 構造体のサブセットにアクセスするだけであっても、代わりに配列構造体配列 (AOSOA) データ構造を使用したほうが良いケースもあります。 そうすることで、外側では局所性の利点を活用し、最も内側ではユニットストライドにできます。 ユニットストライドでベクトル化をフル活用するため、内側の配列長はベクトル長の小さな倍数にすることができます。 各構造体要素の複数のフィールドは、このレイアウト (小さな配列) になります。 外側は、(より大きな) 構造体配列にすることができます。 このレイアウトでは、フィールドアクセスがまだ十分に近いため、オリジナルのコードの隣接する構造体要素へのアクセスにおいてページの局所性が得られます。
以下は、各形式の違いを示すサンプルコードです。
AOS 形式 (構造体配列):
| 例 |
|---|
struct node {
float x, y, z;
};
struct node NODES[1024];
float dist[1024];
for(i=0;i<1024;i+=16){
float x[16],y[16],z[16],d[16];
x[:] = NODES[i:16].x;
y[:] = NODES[i:16].y;
z[:] = NODES[i:16].z;
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i:16] = d[:];
} |
SOA 形式 (配列構造体):
| 例 |
|---|
struct node1 {
float x[1024], y[1024], z[1024];
}
struct node1 NODES1;
float dist[1024];
for(i=0;i<1024;i+=16){
float x[16],y[16],z[16],d[16];
x[:] = NODES1.x[i:16];
y[:] = NODES1.y[i:16];
z[:] = NODES1.z[i:16];
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i:16] = d[:];
} |
AOSOA 形式 (配列構造体配列またはタイル化された構造体配列):
| 例 |
|---|
struct node2 {
float x[16], y[16], z[16];
}
struct nodes2 NODES2[64];
float dist[1024];
for(i=0;i<64;i++){
float x[16],y[16],z[16],d[16];
x[:] = NODES2[i].x[:];
y[:] = NODES2[i].y[:];
z[:] = NODES2[i].z[:];
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i*16:16] = d[:];
} |
多次元のキャスト操作
多次元配列では、C 言語は行優先順を使用します。 コードを配列表記に変更する際に、配列表記では表現できない配列のアクセスパターンに遭遇することはよくあることです。 ほとんどの場合、配列を適切な形式に変換することができます。
例えば、4x4 配列の真ん中のデータにアクセスする場合について考えてみましょう。
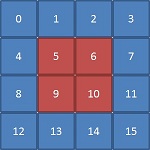
4x4 配列は、次のように 2 次元の配列として表現できます。

この 2 次元のデータを 1 次元の配列として表現しているコードを配列表記に変更する場合、配列を 2 次元配列に変換しない限り、配列表記だけではこのアクセスパターンを表現することはできません。 まず、次のようにコードを変更します。
float (*array_2D)[4] = (float (*)[4])array_1D;
これにより、次のように、配列表記を使用して上記のアクセスパターンを表現できるようになります。
array_2D[1:2][1:2];
次に示すように、この方法は任意の次元に適用できます。
| 例 |
|---|
#define XRES 48 #define YRES 64 #define ZRES 48 float (*array_3D)[YRES][XRES] = (float (*)[YRES][XRES])array_1D; array_3D[1:ZRES-2][1:YRES-2][1:XRES-2]; |